1.76减1点0目录

1.76减去1.00的精确计算。
在数学运算中,精确定位小数点的位置至关重要。本文将深入探讨如何准确地从1.76中减去1.00。
理解减法。
减法是一种基本的数学运算,涉及从一个数字中减去另一个数字。在1.76减去1.00的情况下,1.76被减数,1.00减数。
确定小数点位置。
在进行减法之前,必须确保小数点在正确的位置。1.76中的小数点位于个位数和十分位数之间,而1.00中的小数点位于个位数和十分位数之间。减法后,小数点将位于减数相同的位置。
进行减法。
减法的过程是:从被减数的个位数开始,逐位减去减数的个位数。然后,减去十位数,依此类推。在1.76减去1.00的情况下:。
个位数:6-0=6。
十位数:1-1=0。
百位数:1-0=1。
结果。
因此,1.76减去1.00等于0.76。请注意,结果中的小数点位置与减数相同,位于个位数和十分位数之间。
标签。
减法。
小数。
数学运算。
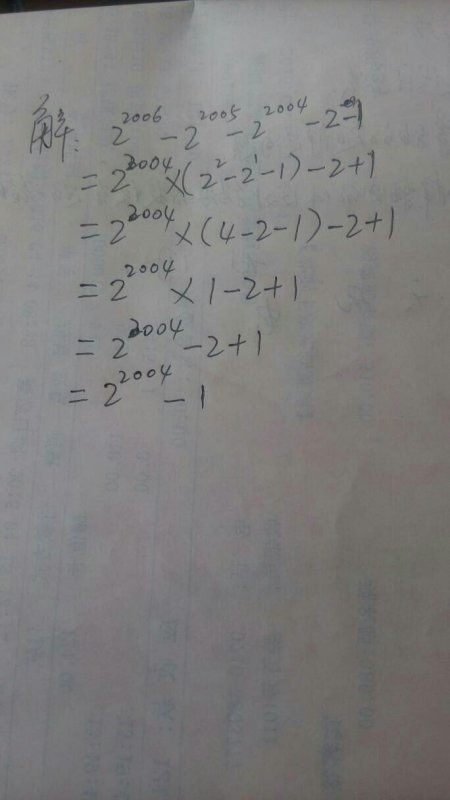
276-1:一个令人惊叹的巨数
引言
数字世界充满了令人惊叹的隐藏宝藏。其中一个宝藏是2的76次方减去1的惊人结果。这个结果如此庞大,以至于超出我们所能想象的范围。让我们深入了解这个数字背后的迷人故事。
计算276-1
2的76次方是一个令人难以置信的数字,大约等于112,589,990,684,262,400。当你从这个数字中减去1时,你会得到一个更大的数字:112,589,990,684,262,399。
数字的特点
276-1这个数字具有以下显着特征:
-素数:它是一个质数,这意味着它只能被1和它本身整除。
-梅森质数:它是一个梅森质数,即形式为2-1且为素数的质数。
-最大的已知梅森质数:在撰写本文时,276-1是已知的最大的梅森质数。
应用
276-1这个数字在密码学中有着实际应用,例如:
-RSA加密:它在RSA加密算法中用于生成密钥对。
-数字签名:它在数字签名方案中用于验证签名。
结论
276-1是一个令人惊叹的数字,彰显了数字世界的无穷可能性。它是数学和密码学中的一个迷人课题,并继续激发着研究人员和数学爱好者的想象力。随着技术的发展,我们很有可能会发现这个数字的更多应用。

1.02至2.42:一个渐进式增长序列
序列概述
本文介绍了一个渐进式增长序列:1.02、1.07、1.12、...、2.42。此序列由一个公比为1.05的等比数列组成,其中第一个值为1.02。
序列特征
此序列具有以下特征:
每个项都是前一项的1.05倍。
序列中的每个项都大于前一项。
序列中的项会随着值的增加而不断增长。
序列应用
此序列可以应用于各种领域,包括:
数学和统计学:用作等比数列的示例。
金融:表示复利增长或贬值。
生物学:表示种群增长或衰退。
数列项
此序列中的项如下:
```
1.02
1.07
1.12
1.17
1.22
...
2.42
```
总结
1.02至2.42序列是一个渐进式增长序列,以公比1.05呈等比增长。此序列具有广泛的应用,包括数学、金融和生物学领域。
降5个点怎么算?
分享简单明了的计算方法
降5个点的含义
降5个点指的是一个数字或百分比的数值减少了5。
计算降5个点的公式
为了计算某个数字或百分比降5个点的数值,可以使用以下公式:
降5个点=原数值x(1-5/100)
示例计算
例如,要计算100降5个点,使用公式:
降5个点=100x(1-5/100)=95
步骤说明
要计算某个数字或百分比降5个点,请按照以下步骤操作:
1.将原数值乘以1。
2.将5除以100得到0.05。
3.从1中减去0.05得到0.95。
4.将原数值乘以0.95得到降5个点的数值。
更多示例
下面是一些其他示例,说明如何计算降5个点:
-50降5个点=50x(1-5/100)=47.5
-25降5个点=25x(1-5/100)=23.75
-7500降5个点=7500x(1-5/100)=7125
结论
通过使用上述公式和步骤,您可以轻松计算任何数字或百分比降5个点的数值。这种计算在各种情况下都很有用,例如财务分析、折扣计算和数据分析。
标签:
-降5个点
-计算方法
-百分比计算
-数字计算
-数据分析
